About

現代の情報化社会が抱える大部分の問題は、センサー、画像、音声などによって収集された多種類の大量のデータの解析、そして情報処理技術によって解決されることが期待されています。しかしながら、データ量が膨大であるため、超大型コンピュータを使用しても解決が容易でないものばかりです。このような問題を解決するためには、アルゴリズムの革新が必要不可欠であり、計算モデルと数理の探求に基盤をおく革新的アルゴリズム設計技法の構築や体系化は、科学の共通基盤として最優先の意義を持ちます。
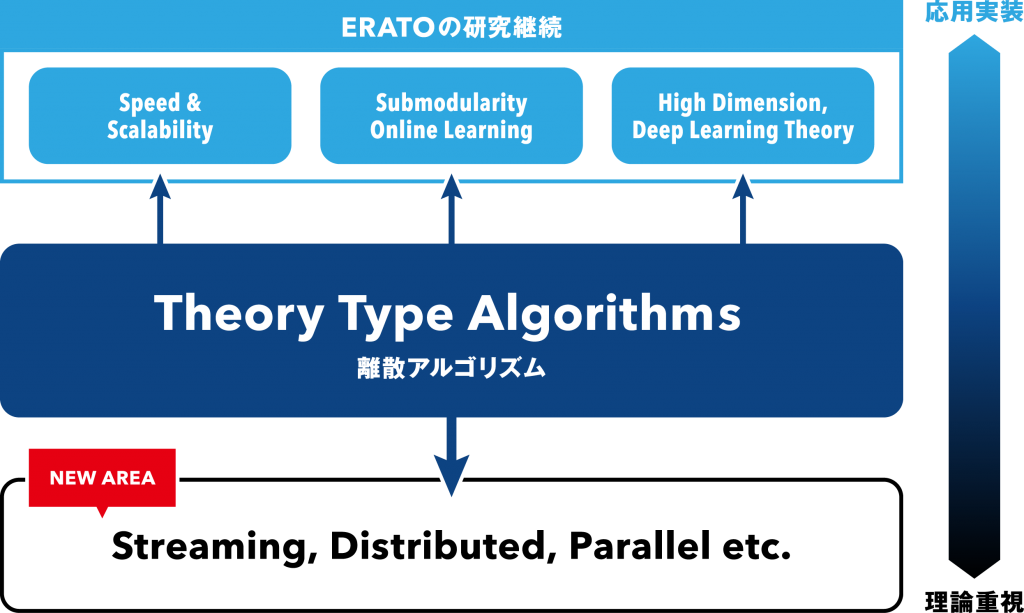
本研究では、以上の背景のもと、数学的理論を駆使することにより、アルゴリズムの理論分野（おもにグラフアルゴリズム）の強化および、理論分野の道具を利用によるアルゴリズムの高速化・スケール化に挑みます。

以下の3点の研究課題を中心にする予定です。

1. 劣モジュラ関数とその応用
   劣モジュラ性は普遍的な概念であり、これまでに扱われてきた機械学習、人工知能分野だけではなく、自然言語、コンピュータビジョンにも応用されています。本提案では、近似アルゴリズム設計手法や代数的手法などさまざまな組合せ最適化手法を取り入れることでロバスト最適化（最悪時の解の質を担保する）などの、実社会に出現する最適化問題の解決に取り組みます。
2. 基礎数理理論の探求：有向グラフマイナー理論
   グラフ理論における最も重要な理論体系「グラフマイナー理論」を用いた効率的なアルゴリズムの設計は、従来のアルゴリズム理論をはるかに深化させることが過去20年で明らかになってきました。しかしながら従来のグラフマイナー理論およびそれに基づくアルゴリズムは、すべて無向グラフにおけるものであり、有向グラフで同様の議論を展開することは困難であると考えられてきました。本研究では、有向グラフ版グラフマイナー理論の構築を目指します。
3. グラフ彩色問題
   離散数学の中心的課題「４色定理、そして曲面上に埋め込まれたグラフに対するグラフ彩色問題」に対する本質的貢献を目指します。